一筆畫、可尼斯堡七橋問題等趣味數學etc
本文發表於 2010 年 12 月 16 日 09:34大家也許都玩過一筆畫,但你知道為什麼有些圖形訂以一筆畫,有些圖形不可以嗎?如果不知道,那我們從頭開始玩吧!
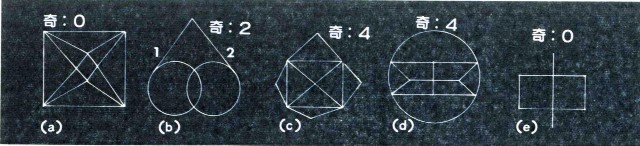
上面這些圖形那些可以一筆畫?那些不可以?請仔細的試一試,對於可以一筆畫者,請找出有無特點,並比較與不可一筆畫圖形的差別。
經過一連串的試驗之後,我們發現 (a) (b) (e)可以一筆畫,而(c) (d)則不能一筆畫,它們之間有什麼差別呢?我們的辦法是把每一個頂點切下來,看看由頂點向外伸出的線段有多少?圖 (a) 八個頂點向外伸出的線段有 4 條;圖 (b) 向外伸出的線段, 2 條者有 l 頂點, 3 條者有2頂點, 4 條者有 2 頂點;圖 (c) 頂點向外伸出的線段, 2 條的有 4 頂點, 4 條者 l 頂點, 5 條者 4 頂點;圖 (d) 頂點向外伸出的線段, 3 條者 4 頂點, 4 條者 5 頂點;圖 (e) 頂點向外伸出的線段, 2 條者 4 頂點, 4 條者 2 頂點,中字的一豎,其起筆與提筆都不算頂點,所謂頂點是二線段的交點。
我們再來看看這些頂點分支的情形(向外伸出的線段數),是不是決定可不可以一筆畫的因素呢?圖 (a) 頂點分支的情形都是偶數,我們對於頂點分支是偶數的稱為偶頂點,八頂點都是偶頂點,圖 (b) 偶頂點有 3 ,奇頂點(頂點向外伸出線段是奇數)有 2。圖 (c) 偶頂點有 5 ,奇頂點有 4 ,圖 (d) 偶頂點有 5 ,奇頂點有 4 。圖 (e) 偶頂點有 6 。從上面偶頂點與奇頂點的分析,我們可以大膽的假設: 一個圖形如果全是偶頂點,一定可以一筆畫。如果奇項點超過 2 個以上,則不能一筆畫。為什麼?
我們知道一筆畫的圖形可以分成兩類,一是起點與終點同一點,如圖 (a) ,另外是起點與終點不同一點,如圖 (b) 。先談起點與終點同一點的情形,既然起點與終點同一點,則此點必是偶頂點,為什麼?因為由此點開始,中間可能有好幾次是「回來」又「出去」,最後才回到此點,即有出有回,那一定有偶數的線段,才能如此。起點與終點同一點,那麼其他的頂點就稱為路過點,而路過點也是偶數點,為什麼?因路過點只是路過而已,進入頂點馬上就離開,有「一進」就有「一出」,那當然要有偶數線段才能辦得到。所以圖形全是偶頂點的可以一筆畫。
其次談一談起點與終點不是同一點的情形,如圖 (b) 的頂點 l 為起點,雖然路線曾經回來,但立刻就離開,所以起點是奇頂點,同理終點也是奇頂點;因為能一筆,的頂點只有一個起點及一個終點,故奇頂點只能有 2 個的圖形才能一筆畫。奇頂點的數目一定是偶數, 4 個奇頂點可以 2 筆畫, 6 個奇頂點可以 3 筆畫。
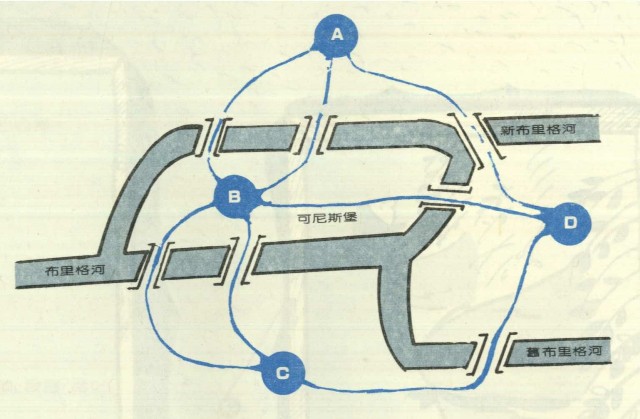
可尼斯堡七橋(Seven Bridges of Königsberg):18世紀時,在可尼斯堡(德國哲學家康德生於此)有七座橋橫跨布里格河,如圖,七橋連繫了河中的兩島,同時也連接河的兩岸,長久以來,可尼斯堡人對於一個人是否能一次走完這七座橋,而不重覆其中任何一座橋,感到懷疑。這問題後來傳到尤拉(十八世紀瑞士天才數學家)耳中,他並沒有到可尼斯堡去親身走一趟,只是在紙上畫出七座橋的位置,試試看能不能一次走完七座橋,他發現這個問題隱藏著重要的科學原則,並提出一個簡單而巧妙的解答來。
尤拉想到一次走完七座橋,那可以不要陸地,只要把橋延長,而把陸地縮小,陸地 A 的三座橋交於頂點A,其他如圖所示,這個問題由雜亂無章變成一筆畫的問題,頂點 A 、 B 、 C 、 D 皆為奇頂點,依上面所述, 4 個奇頂點的圖形要二筆畫才行,尤拉就用數學證明了可尼斯堡七橋問題是不可能的。
尤拉解決了可尼斯堡七橋問題,替拓樸學(註)作了催生的工作,尤拉死後七十年,探討拓樸學的論文就不斷發表,而建立了非常可觀的拓樸領域。 1972 年法國拓樸學家利用拓樸學的成果於各種突變或劇變論(catastrophic theory)的解說很成功,劇變的行為像一隻狗如何突然攻擊或夾著尾巴逃走,或者蘇聯在怎樣的情況之下會突襲美國,因此劇變理論的研究備受各方重視。
註:拓樸學又稱位置解析學,是一種研究形狀變換的數學,如一個化學土做的圓球,可以捏成立方體或一條香蕉,其拓樸性質不變,仍然是「一團」。拓樸學的題材有一筆畫、迷宮、哈哈鏡、繩結等。
【版主註】趣味數學意外的受到歡迎,讓我能把以前的文章貼在這裡。而一些呆子駭客竟然發補習班廣告給我,要我去補習初中數學,未免太惡作劇。
趣味數學etc的意思是,在此頁會貼其他問題。
可尼斯堡今在俄羅斯境內
2010-12-21, 2:50 下午
印度的輪迴
美國數學遊戲大師嘉德納(Martin Gardner,1914年11月21日-2010年5月22日)訪問印度時,專程去拜訪他的朋友羊博士,羊博士也是數學遊戲迷,他喜歡用簡單的四則運算來玩數學遊戲。印度是文化古國,在數學方面也都表現了善長運算的特性。我們都知道輪迴的說法,起源於印度,後來才傳到世界各國;所謂輪迴,是說一個人如果在這世作惡,則來世必會得到報應,為了這世所作之惡而受苦,一直到他的惡業所負的債還清為止,印度人為了不淪入這輪迴中,勸人苦修為善,提高精神生活層次。
話說嘉德納與羊博士寒喧一陣後,羊博士準備好汽車,帶大師去參觀印度的教堂和神祕的宗教儀式,大師看得目體口呆,一天繁忙的參觀後,羊博士招待從美國來的貴賓,吃了一餐咖哩飯。羊博士:「吃過晚飯,到我的書房來,開始真正的大餐 。」嘉德納:「謝謝,我知道你很好客,不然我就不會打擾您了。」
在羊博士的書房裹,嘉德納看到奇奇怪怪的東西,不少是雜亂的擺著,他還找不到一塊可以坐的地方。羊博士:「只要不弄亂我的東西,您高興怎麼坐,就怎麼坐,盡量輕鬆自然。」大師在書堆中,好不容易擠出一點空間來,剛好讓他能坐下來。
羊博士:「您有沒有掌上型電子計算器?」大師從口袋拿出12位的電子計算器,並準備了一張紙。
羊博士:「這個遊戲是這樣的,您隨便選兩個數,將後面的那一數加 1 ,這個和用前一數來除,得到的商記為第三數,然後,把第二數第三數依前述的方法計算,如此繼續下去,看會發生什麼結果?」
嘉德納在紙上寫上他最喜歡的數 3.1415926 ,然後寫下 76 ,他依照羊博士的規則,把 76 加 l 得 77 , 77÷ 3 • 1415926 = 24.5098616542 作為第三數,第三數加 l 後除以 76 , 25.5098616542 ÷ 76 = 0.33565607439 作為第四數, 1.33565 607439 ÷ 24.5098616542 = 0.05449463947 為第五數, 1.05449463947 ÷ 0.33565607439 = 3.141 5926006 為第六數, 4.1415926006 ÷ 0.0544946 3947 = 76 . 0000000161 為第七數。
嘉德納算完之後,感到很奇怪,他知道這種計算器往往會產生尾數誤差,所以第六數實際上就是第一數,第七就是第二數。顯然的,用這規則來算,會得到循環的現象。嘉德納再隨便選兩個數為 5 , 3 ,依規則計算得到 5 , 3 , 0.8 , 0.6 , 2 , 5 , 3 的結果。
嘉德納:「羊博士,這是您的印度魔法?」
羊博士:「哈哈,數學就是數學,沒有魔法,只有簡單的除法,哈哈哈 • • • •。」
經過兩次任選二數而得到同樣的循環現象,這中間一定有道理存在,嘉德納以 a , b 分別代表第一、二數,他在紙上寫下:
第三數 (b+1)÷a=(b+1)/a
第四數 ((b+1)/a +1)÷b=(a+b+1)/ab
第五數 ((a+b+1)/ab+1)÷((b+1)/a)=(a+1)/b
第六數 ((a+1)/b + 1)÷ ((a+b+1)/ab)=a
第七數 (a+1)÷ ((a+1)/b)=b
嘉德納:「哈哈,真是簡單除法,這有點像您們古代的宗教思想 ─ 輪迥,哈哈哈 … … 。」
2010-12-21, 3:15 下午
馬丁. 嘉德納(Martin Gardner,1914年11月21日-2010年5月22日)
美國名聲顯赫的業餘數學大師、魔術師、懷疑論者,他是《科學美國人》雜誌上一個曾開設了20多年的數學遊戲專欄作者。他沒有數學博士學位,但是他的作品能讓廣大普通讀者和數學家也為之著迷。馬丁·加德納才華橫溢,著作頗豐,據不完全統計,迄今已寫了50本以上的書。他曾多次獲獎,包括美國物理學會及美國鋼鐵基金會的優秀科學作者獎。
他生於俄克拉荷馬州的塔爾薩(Tulsa)。1936年,畢業於芝加哥大學哲學系。在進入大學之前,他是一個新教原教旨主義者。通過理性的思考,在大學期間他的信仰消失了,後來他成了一位懷疑論者。畢業後他在家鄉的《民友報》擔任記者。二戰期間,他成為美國海軍的隨軍記者。戰後,他繼續從事自由撰稿人和編輯工作。他的主要工作是1957年到1981年在《科學美國人》的長期專欄作家,他所包辦的「數學遊戲」專欄,成為該雜誌的一個「特色產品」。
【版主再補充】馬丁. 嘉德納是我的最愛,在他所建立的數學遊戲世界,可以讓人忘記不美滿世界。
數學世界是人造觀念中最符合科學原理,期望年輕朋友要親近數學。
馬丁. 嘉德納安息吧,在台灣的粉絲。
2010-12-23, 10:22 上午
阿拉伯人分馬
古代阿拉伯人的數學知識領先歐洲人甚多,這是由於阿拉伯人的計數方式比羅馬人的六十進位計數方式方便太多,這也是後來阿拉伯計數法成為世界通用計數法之故,如果我們仍然採用羅馬人的方法,大家可能對數學一點胃口都沒有了,我們現在用 365 × 24 ,羅馬人卻用 CCCLXV × XXIV ,至於其乘積就得寫成一長串的英文字母,看了就讓人頭痛。
話說有一個阿拉伯人,他臨終以前,留下遺囑:「要把全部馬的1/2分給大兒子,全部馬的1/3分給二兒子,全部馬的1/9分給屘子(末子)。」這個阿拉伯人只有17匹馬,他死後,三個兒子要遵照父親的遺囑分馬,但 17 不是 2 、 3 、 9 的公倍數,也就是 17 不能被 2 、 3 、 9 整除,而馬又不能分成1/2 或1/3或1/9,除非把馬殺掉,大家分馬肉吃。但馬是他們耕種的工具,非常寶貴,不能殺。兄弟3人想不出如何來分馬。
這件事被鄰村的數學教授沙克聽到了,他騎了他的老馬到三兄弟家,沙克教授說:「我的老馬值不了多少錢,就送給你們吧!現在一共有18 匹馬,好了,老大分1/2得 9 匹馬;老二分1/3得 6 匹馬,老三分去得 2 匹馬,哦!還剩下我那匹老馬,哈哈!我以為要跟老馬說再見呢!哈哈!兄弟們!再見了 • 」沙克教授騎著他的老馬回家去了 。兄弟們都很驚奇沙克教授的分馬法,也很高興把父親留下的難題解決。
但過了半小時後,老三氣呼呼的找老二老大說:「沙克教授不公平,老大分得 9 匹馬, 9除以17:是0.5294 …,這大於父親的遺囑,1/2=0.5,我要求重新分馬。」老大老二被老三這麼一說,也以為老三說得有道理,但沙克是數學教授,不會錯才對,讀者們,你認為誰是誰非呢?
兄弟三人帶著他們的 17 匹馬,到鄰村去找沙克教授。沙克教授:「我不是幫你們解決了嗎?」三兄弟一齊說:「但是 9 除以 17 是 0.5294 ,大於父親的遺囑1/2=0.5。」沙克教授抓抓他的光頭說:「那我該怎麼辦呢?」三兄弟說:「請教授幫我們重新分馬。」
沙克教授說:「這真是難題,原來我的分馬法沒錯,好吧!我們來一點複雜的說明,由於你們的父親留下的遺囑是他的馬的1/2 、1/3、1/9 ,而1/2 +1/3+1/9=17/18是比1小。所以如果不管馬是否可以分成分數之限制,每次都會剩下1/18。
用無窮盡分馬術,第一次分馬3人分別得17/2 、 17/3 、 17/9剩下17/18匹馬。
第二次分馬3人分別得17/(2×18) 、17/(3×18) 、17/(9×18) 剩下17/18×18匹馬。
依此類推,繼績下去的分馬如下
從上表可發現,剩餘的「馬」越來越小,如果你能繼續分下去,最後的剩餘會是 0,由於剩餘越來越小,所能分得的也越來越小,我們來看看老大分到多少匹馬,把他每次分到的求總和
17/2 + 17/(2×18) + 17/(2×18×18) + 17/(2×18×18×18) +…
=17/2〔1 + 1/18 + 1/(18×18) +1/(18×18×18) +…〕
=17/2 × 18/17
=9
由於遺囑並沒有剩餘的規定,所以剩餘的部分就得再分,又由於每人比遺囑多分到 9/18 、 6/18 、2/18 ,所以不可用 9 除以 17 來計算分配的比例,從表上的計算,大家可以了解,由於經過無數次的分馬,所以分馬是依遺囑進行。
沙克教授說完,三兄弟高高興興的牽他們分得的馬回家去了。
2011-06-05, 3:38 下午
牛 吃 草
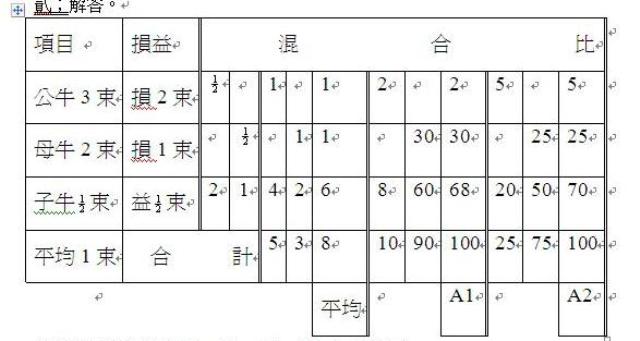
壹;問題。
有一個小牧場,養了100頭牛。臨睡前都會放乾草給牛當夜間的飼料。每頭牛;公牛放3束,母牛放2束,子牛放0.5束,剛好放了100束草。問公牛、母牛、子牛,各有幾頭?
貳;解答。
接下來是混合比的A3、A4、A5、A6,四個解答。
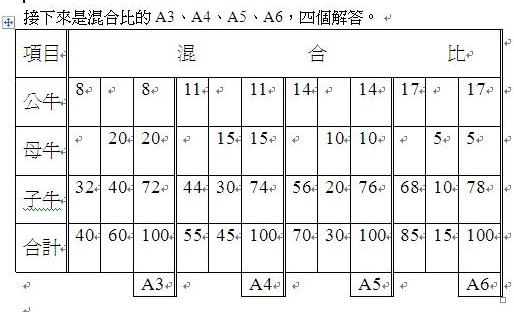
參;答案與驗算。
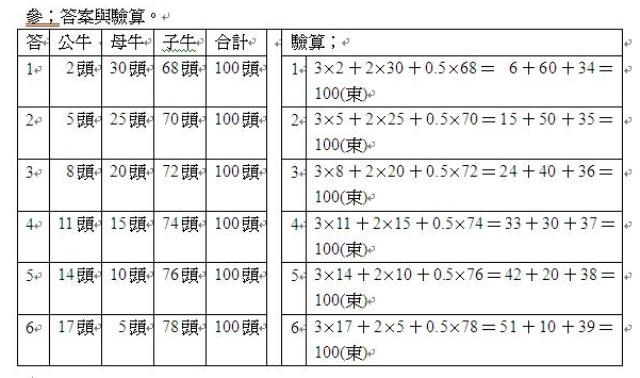
肆;說明。
損和益是所放的草對平均1束來講的。損有兩個,益只有一個;所以益要負抵消兩個損的責任。
把損2和益 對調來比就變成;公牛 比子牛2。損1和益 對調來比就變成;
母牛 比子牛1。(混合比1)
牛沒有 頭的道理,所以把它擴成整數的比;公牛1比子牛4,母牛1比子牛2,是原來的2倍。(混合比2)※如果比有公約數,還要約成最簡的比。
如果間題只要求平均。那麼混合比2就符合8頭牛8束草了。
要100頭牛吃100束草,所以要利用混合比2的兩組比的合計5和3來找出符合湊成100的組合。
第一步是5不變,看3那邊能不能擴成95。當然是不能!
第二步是把5擴成10,看3能不能擴成90?當然是能,30倍就行了。
第三步就看5和3 的最小公倍數是15。以後每增15,3那邊都能配合湊成百了。
5這邊能配合的;第一個是10,第二個是10+15=25,第三個是25+15=40,
第四個是40+15=55,第五個是55+15=70,第六個是70+15=85。
3那邊能配合的;是90(30倍),75(25倍),60(20倍),45(15倍),30(10倍),15
(5倍)。也是六個。
所謂5這邊,就是公牛和子牛的比;是1比4。公牛1頭損2束,子牛4頭益2束。損和益抵消了。
所謂3那邊,就是母牛和子牛的比;是1比2。母牛1頭損1束,子牛2頭益1束。損和益抵消了。
如果把3當這邊,能讓5那邊配合的數的順序是;15、30、45、60、75、90。
(3、6、9、12都不是5的倍數,所以15是第一個)。
5那邊配合的數的順序;是85、70、55、40、25、10了。
這樣的話,A1, A2, A3, A4, A5, A6,六個答的順序就反過來了。
2011-06-07, 8:54 上午
李再興兄這題目很有趣, 是數論的題目!!是在玩自然數(整數)的性質!!
版主通常會用三元一次方程式來解這類問題!!
如何解留給網友自己去做!!
三元一次方程式可以列出2個方程式
及一個條件,答案是自然數(整數)的限制!!!
三元一次方程式只能列出2個方程式
通常稱為不定方程式
也就是說答案通常不是一組
2011-06-09, 1:55 下午
這個問題是於六十多年前,一個學生家長吩咐學生,拿來要我解答的問題。是從很古以前就流傳(口傳)下來的,面臨失傳的算題。那位家長頂多是強記一個答案,存有考考老師的意念吧!
這類問題還有一個,叫做「梨3柿4橄欖七」的問題。純粹是東方的古算術題。日本多種混合的問題,大都要求到「平均」或進一步指定3種物品裡面的一種所占的比,來增加些難度而已。並沒有像這類的「100頭牛吃100束草」及「100元(本來是100文)`買100個水果」的算題。
利用插入表格,使各組比有較密切的發展感是我自己的想法。
多種比例求至平均部份,所參考的是昭和10年4月,日本研數學會編,東京軍事教育研究會發行的受驗參考算術問題正解。
【版主註】東方的古算術題在日本存在,城地 茂是這方面的學者。版主小時候也受到日文算書的影響。
2011-10-28, 1:13 下午
好不容易才把「去九驗算法」有系統的寫完了。詳讀後自己造題演算,然後驗算看看;確實是簡單無比的驗算法。介紹給家人、親朋、同事,甚至留傳給後代學童,相信都有其價值的。祝平安快樂。 2011/10/23 李再興
【SCL註】這是一位年近九十的退休校長,在晨間健走保健的公園相交的晚輩一再提醒下,把他自七十年前開始在小學教算術(數學)的心得留下有系統的文字記錄。算術數學是智慧學習基礎,關心兒童教育者留意,這是簡單無比的驗算法。
【版主註】年近九十的退休校長寫的數學文章,今天貼出,本來想寫一些解說文字,但最近要趕下月在台南大學的國際學術研討會,版主花23年努力,才得到15分鐘的報告機會,會全神灌注在台南大學的國際學術研討會。而且以影像檔方式貼出。
2011-10-28, 5:05 下午
李校長在停用電腦長達四年之後,重拾舊歡,整理出完全的”去九驗算法”,自行打出全文更是令晚生佩服而且自嘆不如。常有以傷眼傷神為由,遠離電腦網路,似非正確!!
2012-02-27, 9:51 上午
90歲的李再興校長的作品:『等律方陣與九宮八卦』
等律方陣和文王八卦的九宮位置完全相同,所以我們知道等律方陣的体裁是依據文王八卦而來。文王八卦又叫做後天八卦。
先天八卦又叫做伏羲八卦,中宮9是相鄰兩個數的和。先天後天兩個的九宮八卦,受方位的影響位置是固定的等律方陣不受方位的影響,最基本的( 1~9)就有8種排列法。
等律方陣九宮格中的數字,是表示有規律的連續數的第幾個的位置;例如你要填的是2、4、6、8、10、12、14、16丶18,一宮要填2,二宮要填4,三宮要填6,九宮要填18了,因為你要填的是2個一數的數字。第一宮要從多少開始由你囉!
3陣(3×3=9宮格的等律方陣)是所有等律方陣的基礎,也是最小的方陣。
5陣(5×5=25宮格的等律方陣)是第二小的等律方陣。
7陣(7×7=49宮格的等律方陣)是第三小的等律方陣,以下類推。
為何沒有4陣和6陣?:因為偶數個宮格沒有中宮(平均數),無法成立等律方陣。
分組排列時產生等差和等律差
(2.4.6)(10.12.14)(18.20.22)各組相鄰兩個數的差都是2,這個2就叫做等差。
上面三組的頭一個數是(2.10,18),相鄰兩個數的差都是8,這個8就是等律差。
(按照連續數,(2,4,6)後應接8,把它改了,所以第二組接第三組也要改)
改變等律差也能寫成等律方陣